fnss.topologies.randmodels.extended_barabasi_albert_topology¶
-
extended_barabasi_albert_topology(n, m, m0, p, q, seed=None)[source]¶ Return a random topology using the extended Barabasi-Albert preferential attachment model.
Differently from the original Barabasi-Albert model, this model takes into account the presence of local events, such as the addition of new links or the rewiring of existing links.
More precisely, the Barabasi-Albert topology is built as follows. First, a topology with m0 isolated nodes is created. Then, at each step: with probability p add m new links between existing nodes, selected with probability:

with probability q rewire m links. Each link to be rewired is selected as follows: a node i is randomly selected and a link is randomly removed from it. The node i is then connected to a new node randomly selected with probability
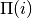 ,
with probability
,
with probability 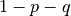 add a new node and attach it to m nodes of
the existing topology selected with probability
add a new node and attach it to m nodes of
the existing topology selected with probability 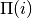
Repeat the previous step until the topology comprises n nodes in total.
Parameters: - n : int
Number of nodes
- m : int
Number of edges to attach from a new node to existing nodes
- m0 : int
Number of edges initially attached to the network
- p : float
The probability that new links are added
- q : float
The probability that existing links are rewired
- seed : int, optional
Seed for random number generator (default=None).
Returns: - G : Topology
References
[1] A. L. Barabasi and R. Albert “Topology of evolving networks: local events and universality”, Physical Review Letters 85(24), 2000.