fnss.topologies.randmodels.barabasi_albert_topology¶
-
barabasi_albert_topology(n, m, m0, seed=None)[source]¶ Return a random topology using Barabasi-Albert preferential attachment model.
A topology of n nodes is grown by attaching new nodes each with m links that are preferentially attached to existing nodes with high degree.
More precisely, the Barabasi-Albert topology is built as follows. First, a line topology with m0 nodes is created. Then at each step, one node is added and connected to m existing nodes. These nodes are selected randomly with probability
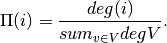
Where i is the selected node and V is the set of nodes of the graph.
Parameters: - n : int
Number of nodes
- m : int
Number of edges to attach from a new node to existing nodes
- m0 : int
Number of nodes initially attached to the network
- seed : int, optional
Seed for random number generator (default=None).
Returns: - G : Topology
Notes
The initialization is a graph with with m nodes connected by
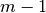 edges.
It does not use the Barabasi-Albert method provided by NetworkX because it
does not allow to specify m0 parameter.
There are no disconnected subgraphs in the topology.
edges.
It does not use the Barabasi-Albert method provided by NetworkX because it
does not allow to specify m0 parameter.
There are no disconnected subgraphs in the topology.References
[1] A. L. Barabasi and R. Albert “Emergence of scaling in random networks”, Science 286, pp 509-512, 1999.